专为高中生提供有价值的资讯
二次方程的求根公式已经为大家整理好了,二次方程,是一种整式方程,其未知项的最高次数是2,且各项未知数的次数只能是自然数。比如根号x加x的平方等于1 ,这样未知数的的次数含有非自然数,就不是一元二次方程了。
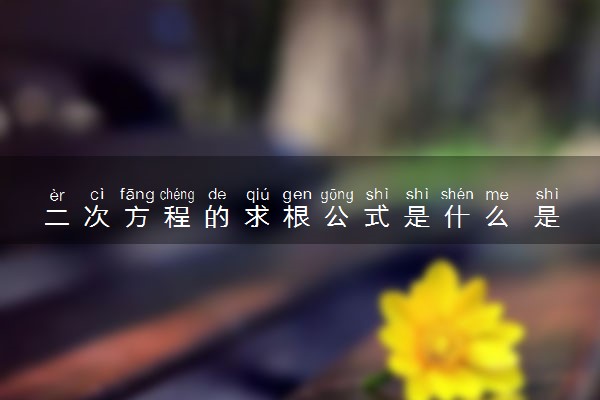
解ax^2+bx+c=0的解。
移项,
ax^2+bx=-c
两边除a,然后再配方,
x^2+(b/a)x+(b/2a)^2=-c/a+(b/2a)^2
[x+b/(2a)]^2=[b^2-4ac]/(2a)^2
两边开平方根,解得
x=[-b±√(b2-4ac)]/(2a)
一元二次方程作为九年级上册数学的第一章,它的主要知识点虽只有四个;但是不少初中小伙伴在学习过程中轻概念和缺少总结的习惯,使得不少人在考试中经常犯错,或者出现卡顿的现象。在此,再次强调学习一元二次方程必须掌握这四个知识点。
学习一元二次方程首先必须掌握它的基本概念,就初中阶段所学的方程分为两类:一类是分式方程;另一类是整式方程。一元二次方程是整式方程的一个类型,它只含一个未知数,且未知数最高指数是2。在解题过程中,当碰到未知数的指数含字母或者二次项系数含字母时,我们就要能用方程的定义来求字母值。
学好一元二次方程的第二个要求就是要会解一元二次方程,一元二次方程属于高次方程;所以我们解题的基本思路就是降次,其主要方法有四种:(1)直接开方法;(2)因式分解法;(3)配方法;(4)公式法。需要能根据方程的基本特征选择恰当的方法。
二次方程,是一种整式方程,其未知项的最高次数是2,且各项未知数的次数只能是自然数。比如根号x加x的平方等于1 ,这样未知数的的次数含有非自然数,就不是一元二次方程了。如果一个二次方程只含有一个未知数 x,那么就称其为一元二次方程,其主要内容包括方程求解、方程图像、一元二次函数求最值三个方面;如果一个二次方程含有二个未知数x、y,那么就称其为二元二次方程,以此类推。
二次方程定义二次方程是一种整式方程,其未知项的最高次数是2。根的判定是利用判别式判定。
如果一个二次方程只含有一个未知数 x,那么就称其为一元二次方程。
如果一个二次方程含有二个未知数 x、y,那么就称其为二元二次方程,以此类推。
二次方程中最常见的是一元二次方程。它的基本表达式为:
二次方程根的判定解实系数一元二次方程时,必须关注解是实数还是复数,通过判断判别式的正负可以判断。
对于任意一个一元二次方程:
(1)若△<0,方程无实数根,有两个复数根:
(2)若△=0,方程有两个相等的实根:
(3)若△>0,方程有两个不等实根:
解一元二次方程的基本思想是设法把所有方程变形成和它同解的两个最简单的一元一次方程
该方法主要是通过因式分解,把一个一元二次方程的求解问题转化为一元一次方程的求解问题,通常把这种方法也叫作降次求解方法,这种方法也适用于某些高次方程。
Copyright 2019-2029 http://www.86gaokao.com 【八六高考】 皖ICP备19022700号-9
声明: 本站 所有软件和文章来自互联网 如有异议 请与本站联系 本站为非赢利性网站 不接受任何赞助和广告